MATEMATİK

“Bilim deyince, onda hakikat diye öne sürdüğü önermelerin pekin olmasını ister; pekinlik ise en mükemmel şekliyle matematikte bulunur. O halde bilim o disiplindir ki; önermeleri matematikle ifade edilir. O zaman matematiği kullanmayan disiplinler bilimin dışında kalacaklardır.”

M.Kemal Atatürk

Klein Şişesi

Blender ile hazırladığım klein şişesi animasyonum

yapım süresi 1saate yakın render süresi 2.5saat

https://youtu.be/8Jr_DpTM3wI

19. yüzyıl Alman matematikçisi August Möbius’un adını taşıyan bir Möbius şeridi kolayca saniyeler içinde yapılabilir. Ortaya çıkan şekil ise, karmaşık geometrik şekillerle ilgili anlayışımızı geliştiren bazı beklenmedik özelliklere sahiptir. Felix Klein ise iki Möbius şeridinden oluşan bir şekil olan Kleinsche Flasche’yi (Klein şişesi) tanımlar…

Möbius Şeridi Nasıl Yapılır?

2dakikada bilim

Normalde bir yüzeyin iki tarafı olur: İçi dışı ya da önü arkası. Ancak Möbius şeridi oluşturulduktan sonra yalnızca bir yüzeye sahiptir. Aslında Möbius şeridi en basit tek taraflı yüzeydir ve bir kağıt şeritten yapılması kolaydır. İsterseniz hemen deneyebilirsiniz. İnce uzun dikdörtgen biçiminde bir kağıt alın. Sonrasında bir yüzünü kırmızı noktalar diğer yüzünü ise yeşil noktalar ile boyayın. Şimdi şeridin iki ucunu alın ve tek bir büküm yaptıktan sonra, kırmızı noktalı taraf yeşil noktalı tarafla birleşecek şekilde 180 derece çevirin. Ardından iki ucu birbirine yapıştırın. Bu bir Möbius şerididir. Bu şeridin yüzeyinde parmağınızı gezdirirseniz kırmızı ve yeşil noktaların her birine dokunabilirsiniz.

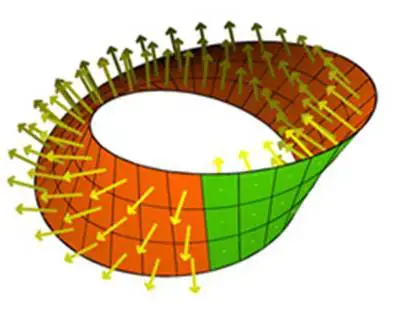
Möbius Şeridi

Elinizdeki şeridi yapıştırdığınız yerden ayırıp, bir kere daha kendi etrafında çevirirseniz aynı sonucu elde edemezsiniz. Ancak 3. defa çevirdiğinizde yine içi dışı aynı olan tek bir yüzeye sahip olursunuz. Genel olarak çift sayıda büküm her zaman iki taraflı bir yüzey üretecektir. Ancak tek taraflı bükümler ise size tek taraflı bir yüzey verecektir.

Basitliğine rağmen Möbius şeridi gerçek bir matematiksel keşifti. Topoloji, şekillerin sürekli eğilme ve esneme altında değişmeyen özelliklerini araştıran matematik disiplinidir. Yüzeylerin yönlendirilebilirliği hakkında akıl yürütme, topolojide yüzeyleri ve manifoldları anlamanın ve sınıflandırmanın anahtarlarından biridir. Möbius şeridi, üç boyutlu uzayda oluşturulabilen en basit, yönlendirilemeyen, iki boyutlu yüzeydir.

Klein Şişesi

Klein şişesi 1882’de Felix Klein tarafından keşfedildi. O zamandan beri de popüler matematiksel şekiller arasında varlığını koruyor. Klein şişesi de, Möbius şeridinin tuhaf özelliklerini taşıyan 3 boyutlu geometrik bir nesnedir. Normal olarak bir şişenin bir iç bir de dış yüzeyi olması gerekir. Ancak bu Klein şişesi için geçerli değildir. Bu şişenin de tek bir yüzü vardır yani aslında iç yüzeyi ve dış yüzeyi birdir. Ayrıca Klein şişesinin, kendi gövdesini delip “içine” giren, oradan da “dibine” açılan bir de boynu vardır.

Klein Şişesi nedir
Akıllara durgunluk veren tasarımı, esasen birbirine bağlı iki Mobius şeridinden oluşuyor.

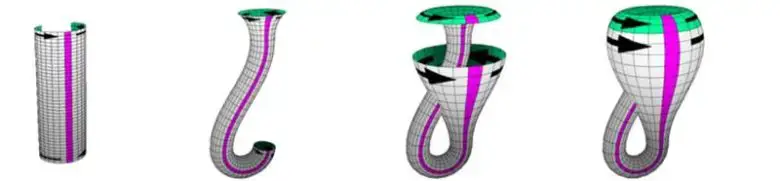
Klein Şişesi Nasıl Yapılır?

klein şişesini gösteren bir animasyon

Möbius Şeridini yaparken, dikdörtgen biçimindeki şeridi uçlarından 180 derece ters olacak şekilde yapıyorduk. Klein Şişesi de bir silindiri aynı biçimde 180 derece ters olacak şekilde birleştirilerek elde edilir.

Klein şişesi, bir silindir oluşturmak için esnek bir tabakanın iki tarafının birleştirilmesiyle başlar.

Felix Klein 1880’de Leipzig’de profesör olduğunda bu şişeyi derslerde kullanılacak bir geometrik model olarak tasarlamıştı. Bu nedenle günlük yaşamda bir işleve sahip değildir. Ancak artistik bir biblo olmanın ötesinde önemli bir matematiksel değer taşır. Klein şişesi yalnızca dört boyutlu uzayda bulunur, ancak bir Klein şişesinin modeli üç boyutlu olarak yapılabilir. Ancak bu model orijinal modelden farklıdır çünkü bir noktada şekil kendine temas etmek zorundadır. Ancak dört boyutlu uzayda durum bu biçimde değildir.

Klein şişesinin tuhaf özellikleri sayısız topoloji problemine olduğu kadar, sanat yapıtlarına, bulmacalara da ilham kaynağı olmuştur. Bu eser Alan Bennett’in İngiltere’nin Bedford Bilim Müzesi için yaptığı Klein şişesi dizisinden biridir. Eser birbirine geçmiş 3 Klein şişesinden oluşmaktadır.

kaynakça